Resolviendo Problemas del Teorema de Pitágoras para 2º ESO: Guía Completa y Ejemplos Prácticos
El Teorema de Pitágoras es uno de los pilares fundamentales de la geometría y un concepto esencial que los estudiantes de 2º de ESO deben dominar. Este teorema no solo es crucial para las matemáticas, sino que también tiene aplicaciones prácticas en la vida cotidiana, desde la construcción hasta el diseño gráfico. Si alguna vez te has preguntado cómo calcular la longitud de un lado de un triángulo rectángulo o cómo aplicar este teorema a situaciones del mundo real, estás en el lugar correcto. En esta guía completa, resolveremos problemas del Teorema de Pitágoras, explicaremos sus fundamentos y te ofreceremos ejemplos prácticos que facilitarán su comprensión. Prepárate para adentrarte en el fascinante mundo de la geometría!
1. ¿Qué es el Teorema de Pitágoras?
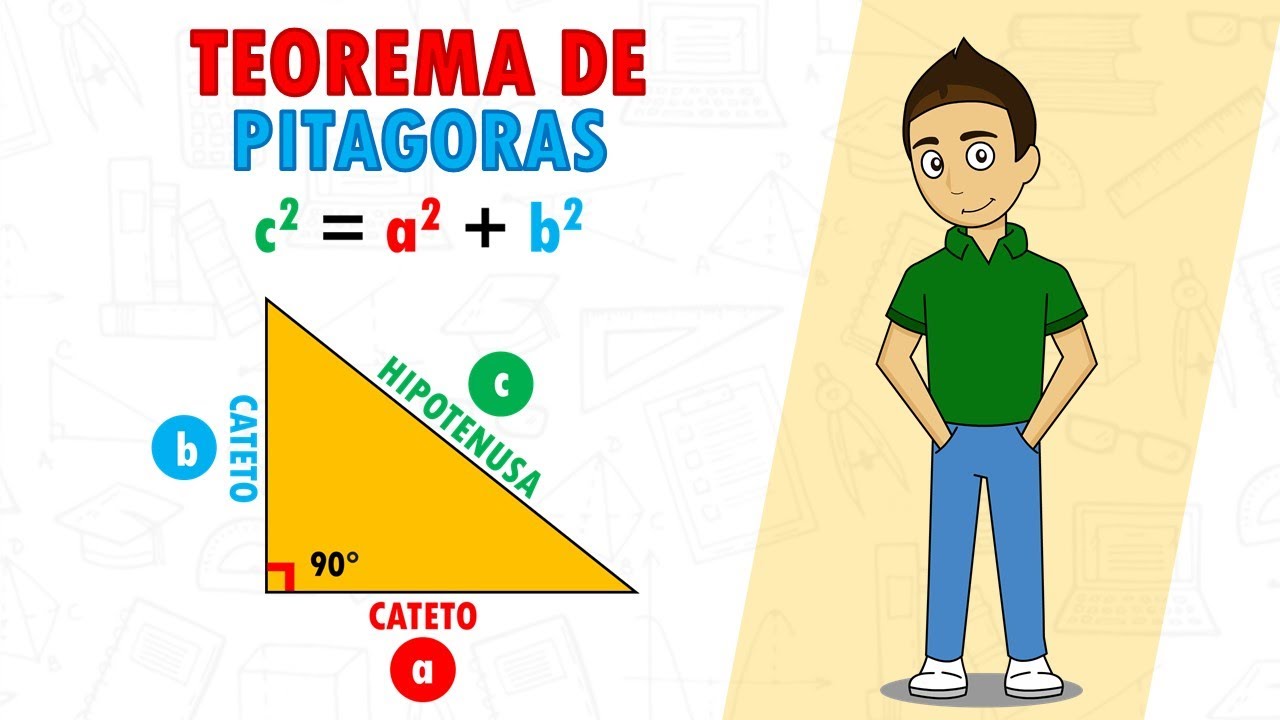
El Teorema de Pitágoras establece una relación entre los lados de un triángulo rectángulo. En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa, mientras que los otros dos lados se conocen como catetos. La fórmula del teorema se expresa como:
- a² + b² = c²
Donde c es la longitud de la hipotenusa, y a y b son las longitudes de los catetos. Este teorema nos dice que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Esta relación es útil para resolver problemas en diversas áreas, desde la arquitectura hasta la navegación.
1.1 Origen del Teorema
El Teorema de Pitágoras lleva el nombre del matemático griego Pitágoras, quien vivió en el siglo VI a.C. Aunque se le atribuye su descubrimiento, evidencias sugieren que este conocimiento ya existía en civilizaciones anteriores, como en Babilonia y Egipto. La simplicidad y elegancia del teorema han hecho que perdure a lo largo de los siglos, convirtiéndose en una herramienta esencial en matemáticas.
1.2 Aplicaciones Prácticas
Las aplicaciones del Teorema de Pitágoras son numerosas. En la vida cotidiana, se utiliza para:
- Calcular distancias entre dos puntos en un plano.
- Determinar la altura de un objeto usando la sombra y la distancia.
- Diseñar estructuras arquitectónicas.
Por ejemplo, si un arquitecto necesita saber la longitud de una escalera que se apoyará en una pared, puede usar el Teorema de Pitágoras para calcularlo de manera precisa.
2. Cómo Resolver Problemas con el Teorema de Pitágoras
Resolver problemas utilizando el Teorema de Pitágoras requiere un enfoque metódico. A continuación, te explicamos los pasos a seguir para abordar cualquier problema relacionado con este teorema.
2.1 Identificación de los Elementos del Triángulo
El primer paso es identificar qué lados del triángulo son los catetos y cuál es la hipotenusa. Recuerda que la hipotenusa siempre es el lado más largo y está opuesto al ángulo recto. Asegúrate de tener claros los valores de los catetos antes de aplicar la fórmula.
2.2 Aplicación de la Fórmula
Una vez que hayas identificado los lados, sustituye los valores en la fórmula del teorema:
- Si conoces los catetos, calcula la hipotenusa:
- Ejemplo: Si a = 3 y b = 4, entonces c² = 3² + 4² = 9 + 16 = 25, por lo que c = 5.
- Si conoces la hipotenusa y uno de los catetos, despeja la fórmula para encontrar el lado desconocido:
- Ejemplo: Si c = 10 y a = 6, entonces 10² = 6² + b², lo que da 100 = 36 + b², y b² = 64, por lo que b = 8.
2.3 Verificación de Resultados
Después de realizar los cálculos, es importante verificar los resultados. Revisa si los valores obtenidos tienen sentido en el contexto del problema y asegúrate de que se cumpla la relación del Teorema de Pitágoras.
3. Ejemplos Prácticos de Problemas del Teorema de Pitágoras
Para solidificar tu comprensión del Teorema de Pitágoras, veamos algunos ejemplos prácticos que ilustran su aplicación.
3.1 Ejemplo 1: Encontrar la Hipotenusa
Imagina que tienes un triángulo rectángulo donde uno de los catetos mide 6 metros y el otro 8 metros. Queremos encontrar la longitud de la hipotenusa.
- Usamos la fórmula: c² = a² + b².
- Por lo tanto, c² = 6² + 8² = 36 + 64 = 100.
- Entonces, c = √100 = 10 metros.
En este caso, la hipotenusa mide 10 metros.
3.2 Ejemplo 2: Encontrar un Cateto Desconocido
Ahora, supongamos que conocemos la hipotenusa y uno de los catetos. La hipotenusa mide 13 metros y uno de los catetos mide 5 metros. ¿Cuál es la longitud del otro cateto?
- Aplicamos la fórmula: 13² = 5² + b².
- Esto se traduce en 169 = 25 + b², lo que implica que b² = 144.
- Por lo tanto, b = √144 = 12 metros.
Así que el otro cateto mide 12 metros.
4. Problemas Comunes y Errores a Evitar
Al resolver problemas del Teorema de Pitágoras, es fácil cometer errores comunes. Aquí discutimos algunos de ellos y cómo evitarlos.
4.1 Confundir los Lados
Un error común es confundir la hipotenusa con los catetos. Recuerda que la hipotenusa siempre es el lado opuesto al ángulo recto y es el más largo. Asegúrate de identificar correctamente cada lado antes de realizar cualquier cálculo.
4.2 Olvidar el Despeje de la Fórmula
Cuando intentas encontrar un cateto a partir de la hipotenusa y el otro cateto, es crucial despejar la fórmula correctamente. Asegúrate de restar el cuadrado del cateto conocido de la hipotenusa antes de aplicar la raíz cuadrada.
4.3 No Verificar los Resultados
Siempre verifica tus resultados. Si obtienes un valor negativo o un número que no tiene sentido en el contexto del problema, revisa tus cálculos. La verificación te ayudará a evitar errores y a asegurarte de que tus respuestas sean correctas.
5. Aplicaciones Avanzadas del Teorema de Pitágoras
Más allá de los problemas básicos, el Teorema de Pitágoras tiene aplicaciones avanzadas en diversas disciplinas. Veamos algunas de ellas.
5.1 En Arquitectura y Construcción
En arquitectura, el Teorema de Pitágoras es fundamental para asegurar que los ángulos de las estructuras sean correctos. Por ejemplo, al construir un edificio, los arquitectos utilizan este teorema para verificar que las esquinas sean rectas, lo que se conoce como el «triángulo de 3-4-5». Este método asegura que los lados midan 3 y 4 unidades, y la hipotenusa mida 5 unidades, formando un triángulo rectángulo perfecto.
Los navegantes también utilizan el Teorema de Pitágoras para calcular distancias entre dos puntos en un mapa. Si conoces la distancia en línea recta entre dos puntos y las distancias horizontales y verticales, puedes aplicar el teorema para encontrar la distancia real en el terreno. Esto es esencial para la planificación de rutas y la navegación precisa.
5.3 En Tecnología y Diseño Gráfico
En el ámbito del diseño gráfico y la tecnología, el Teorema de Pitágoras se utiliza para calcular dimensiones y distancias en gráficos digitales. Por ejemplo, al crear un diseño, puedes necesitar calcular la distancia entre dos puntos en un plano, asegurando que los elementos estén correctamente alineados y proporcionados.
6. Preguntas Frecuentes (FAQ)
¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es aquel que tiene un ángulo de 90 grados. En este tipo de triángulo, se aplica el Teorema de Pitágoras, que relaciona las longitudes de sus lados. Este tipo de triángulo es esencial en la geometría y tiene muchas aplicaciones en la vida real.
¿Cómo puedo recordar la fórmula del Teorema de Pitágoras?
Una manera fácil de recordar la fórmula a² + b² = c² es pensar en un triángulo rectángulo y visualizar los lados. Puedes recordar que los catetos (a y b) se suman para igualar el cuadrado de la hipotenusa (c). Hacer diagramas y practicar problemas te ayudará a internalizar esta relación.
¿El Teorema de Pitágoras se aplica a todos los triángulos?
No, el Teorema de Pitágoras solo se aplica a triángulos rectángulos. Para triángulos que no son rectángulos, se requieren otras fórmulas, como la Ley de los Senos o la Ley de los Cosenos, que se utilizan en trigonometría.
¿Cómo puedo practicar más problemas del Teorema de Pitágoras?
La práctica es clave para dominar el Teorema de Pitágoras. Puedes encontrar problemas en libros de texto, recursos en línea o incluso crear tus propios problemas. Intenta resolver diferentes tipos de problemas, incluyendo aquellos que requieren despejar la fórmula y aplicar el teorema en contextos del mundo real.
¿Qué herramientas puedo usar para resolver problemas del Teorema de Pitágoras?
Para resolver problemas del Teorema de Pitágoras, puedes utilizar calculadoras científicas, software de geometría, o incluso aplicaciones en tu teléfono móvil que te permiten visualizar triángulos y calcular sus lados. Estas herramientas pueden hacer que la práctica sea más interactiva y entretenida.
¿Hay alguna relación entre el Teorema de Pitágoras y la trigonometría?
Sí, el Teorema de Pitágoras es fundamental para la trigonometría. La trigonometría se basa en las relaciones entre los ángulos y los lados de los triángulos, y el Teorema de Pitágoras proporciona una base para entender estas relaciones, especialmente en triángulos rectángulos. Las funciones trigonométricas como seno, coseno y tangente se derivan de estas relaciones y se utilizan en muchas aplicaciones matemáticas.