# Cómo dibujar un ángulo cuyo coseno es el doble que su seno: Guía paso a paso
Dibujar ángulos puede parecer una tarea sencilla, pero hay momentos en los que queremos ser más específicos y trabajar con propiedades trigonométricas. En este artículo, nos centraremos en un caso particular: cómo dibujar un ángulo cuyo coseno es el doble que su seno. ¿Te has preguntado cómo se relacionan estas funciones trigonométricas y cómo puedes visualizarlas? La relación entre el coseno y el seno es fundamental en trigonometría, y entenderla puede abrirte la puerta a una mejor comprensión de las matemáticas en general.
A lo largo de esta guía paso a paso, exploraremos cómo identificar el ángulo que satisface esta condición y cómo dibujarlo de manera precisa. Aprenderás sobre las funciones seno y coseno, resolveremos la ecuación correspondiente y finalmente, te mostraré cómo trazarlo en un sistema de coordenadas. Si estás listo para embarcarte en este viaje matemático, ¡comencemos!
## Comprendiendo las funciones seno y coseno
### ¿Qué son el seno y el coseno?
Las funciones seno y coseno son fundamentales en trigonometría y se utilizan para describir las relaciones entre los ángulos y los lados de un triángulo rectángulo. En un triángulo rectángulo, el seno de un ángulo agudo es la razón entre el cateto opuesto y la hipotenusa, mientras que el coseno es la razón entre el cateto adyacente y la hipotenusa.
Por ejemplo, si consideramos un triángulo rectángulo donde el ángulo es θ, podemos definir:
– Seno (sin θ): ( text{sin } θ = frac{text{cateto opuesto}}{text{hipotenusa}} )
– Coseno (cos θ): ( text{cos } θ = frac{text{cateto adyacente}}{text{hipotenusa}} )
Estas funciones son cíclicas y se repiten cada 360 grados, lo que significa que sus valores varían según el ángulo.
### Propiedades clave
Una de las propiedades más importantes de estas funciones es que están relacionadas a través de la identidad fundamental de la trigonometría:
[ sin^2(θ) + cos^2(θ) = 1 ]
Esto implica que si conocemos el valor de una de estas funciones, podemos calcular el valor de la otra.
## La ecuación a resolver
Para resolver el problema de cómo dibujar un ángulo cuyo coseno es el doble que su seno, necesitamos establecer la ecuación correspondiente. La condición que se nos presenta es:
[ cos(θ) = 2 cdot sin(θ) ]
### Sustituyendo en la identidad trigonométrica
Sustituyendo la relación anterior en la identidad fundamental, tenemos:
1. Reemplazamos ( cos(θ) ) en la identidad:
[ sin^2(θ) + (2 cdot sin(θ))^2 = 1 ]
2. Esto se simplifica a:
[ sin^2(θ) + 4 cdot sin^2(θ) = 1 ]
3. Combinando términos:
[ 5 cdot sin^2(θ) = 1 ]
4. Por lo tanto:
[ sin^2(θ) = frac{1}{5} ]
5. Esto implica que:
[ sin(θ) = frac{1}{sqrt{5}} ]
### Encontrando el coseno
Para encontrar el coseno, utilizamos la identidad fundamental:
[ cos^2(θ) = 1 – sin^2(θ) ]
Sustituyendo:
[ cos^2(θ) = 1 – frac{1}{5} = frac{4}{5} ]
Por lo tanto:
[ cos(θ) = frac{2}{sqrt{5}} ]
## Determinando el ángulo
### Ángulo en radianes y grados
Ahora que tenemos los valores de seno y coseno, podemos utilizar la función inversa para determinar el ángulo θ. Usaremos la función arco seno:
[ θ = arcsinleft(frac{1}{sqrt{5}}right) ]
### Cálculo práctico
Puedes calcular este ángulo utilizando una calculadora científica o software que tenga funciones trigonométricas. El resultado te dará un valor en radianes, que puedes convertir a grados multiplicando por ( frac{180}{pi} ). Recuerda que hay múltiples soluciones para este ángulo debido a la naturaleza cíclica de las funciones trigonométricas.
## Trazando el ángulo en un sistema de coordenadas
### Preparativos para el dibujo
Antes de comenzar a dibujar, es importante tener un sistema de coordenadas bien definido. Asegúrate de tener un eje horizontal (eje X) y un eje vertical (eje Y) dibujados en tu papel o pizarra. El punto de intersección de ambos ejes será el origen (0,0).
### Dibujando el ángulo
1. Marca el ángulo: Desde el origen, utiliza un transportador para marcar el ángulo θ que calculaste. Asegúrate de que el transportador esté alineado correctamente con el eje X.
2. Dibuja la línea: Desde el origen, dibuja una línea que se extienda hacia el ángulo marcado. Esta línea representará la hipotenusa de tu triángulo.
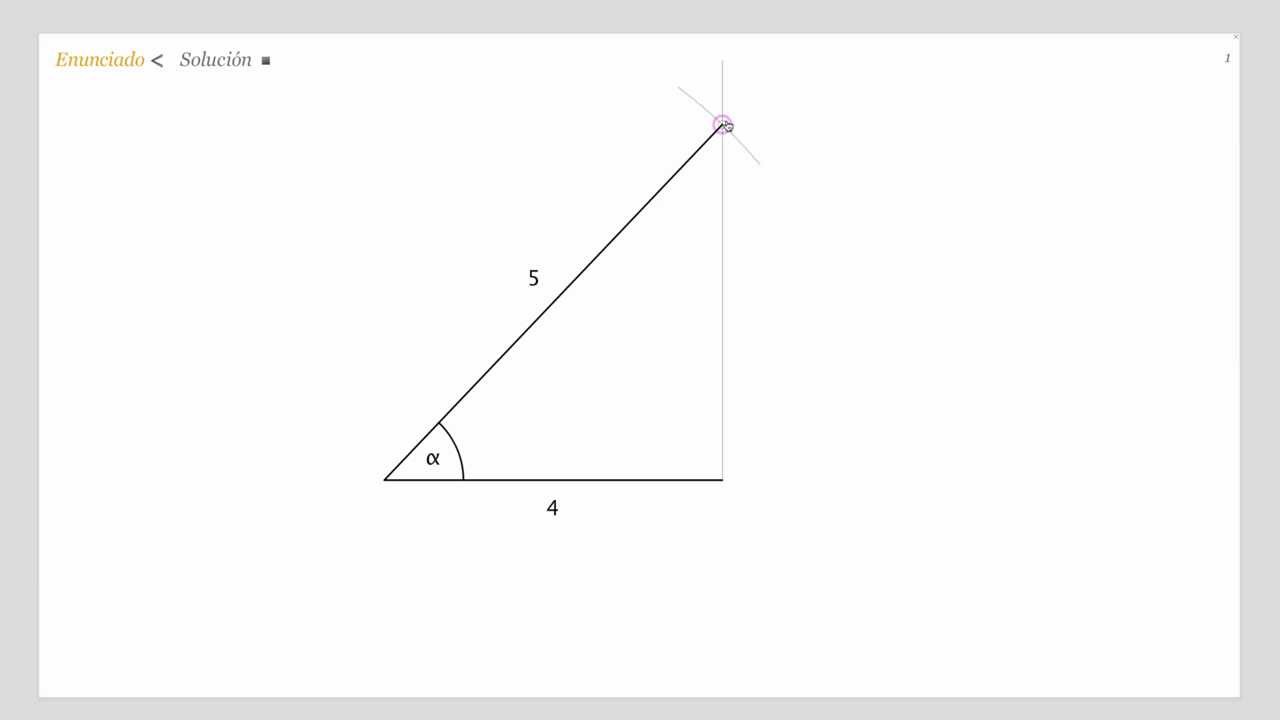
3. Completa el triángulo: Desde el extremo de la línea que dibujaste, baja una línea perpendicular al eje X para formar un triángulo rectángulo. El segmento horizontal será el cateto adyacente y el segmento vertical será el cateto opuesto.
4. Etiquetas: No olvides etiquetar los lados de tu triángulo. El cateto opuesto corresponderá a ( sin(θ) ) y el cateto adyacente a ( cos(θ) ).
## Aplicaciones y ejemplos prácticos
### Aplicaciones en la vida real
Dibujar ángulos cuya relación entre seno y coseno es relevante tiene aplicaciones en diversas áreas, como la ingeniería, la arquitectura y la física. Por ejemplo, al diseñar estructuras, es crucial entender cómo las fuerzas actúan en diferentes ángulos para asegurar la estabilidad.
### Ejemplo práctico
Supongamos que estás trabajando en un proyecto de construcción donde necesitas determinar la inclinación de un tejado. Conocer la relación entre seno y coseno te permitirá calcular la pendiente de manera efectiva, asegurando que el agua drene correctamente y que la estructura sea segura.
## Preguntas Frecuentes (FAQ)
### 1. ¿Cómo puedo encontrar otros ángulos con la misma relación entre seno y coseno?
Puedes utilizar la periodicidad de las funciones trigonométricas. Si has encontrado un ángulo θ, los otros ángulos se pueden calcular sumando o restando múltiplos de 360 grados (o 2π radianes).
### 2. ¿Qué sucede si el coseno no es el doble que el seno?
En ese caso, deberás resolver una ecuación diferente que refleje la nueva relación entre las funciones. Puedes aplicar el mismo proceso que hemos utilizado aquí, ajustando la ecuación según sea necesario.
### 3. ¿Por qué es importante entender la relación entre seno y coseno?
Comprender esta relación es fundamental en trigonometría y tiene aplicaciones prácticas en la resolución de problemas en ingeniería, física y muchas otras disciplinas.
### 4. ¿Puedo usar software para trazar ángulos y triángulos?
Sí, hay diversas aplicaciones y programas que permiten trazar ángulos y triángulos de manera precisa. Estos pueden ser especialmente útiles para visualizar problemas complejos.
### 5. ¿Qué herramientas necesito para dibujar ángulos?
Para dibujar ángulos, necesitarás un transportador, una regla y un lápiz. Si deseas ser más preciso, puedes utilizar software de geometría en línea.
### 6. ¿Cómo afecta el cuadrante en el que se encuentra el ángulo?
El cuadrante en el que se encuentra el ángulo afectará el signo de las funciones seno y coseno. En el primer cuadrante, ambos son positivos; en el segundo, el seno es positivo y el coseno negativo, y así sucesivamente.
### 7. ¿Qué tan preciso debe ser mi dibujo?
La precisión dependerá del propósito de tu dibujo. Si es para un proyecto académico, asegúrate de que sea lo más exacto posible. Si es para un uso general, un dibujo aproximado puede ser suficiente.
Con esta guía, ya tienes las herramientas necesarias para dibujar un ángulo cuyo coseno es el doble que su seno. La trigonometría puede parecer complicada al principio, pero con práctica y comprensión, se convierte en una herramienta poderosa y útil. ¡Anímate a experimentar con otros ángulos y relaciones trigonométricas!