# Cómo se Ubican los Números en la Recta Numérica: Guía Completa y Ejemplos
La recta numérica es una herramienta fundamental en matemáticas que nos permite visualizar y comprender la relación entre diferentes números. Desde la educación primaria hasta niveles más avanzados, la habilidad de ubicar números en esta línea es esencial para resolver problemas, realizar operaciones y entender conceptos más complejos. Pero, ¿alguna vez te has preguntado cómo se ubican los números en la recta numérica? En esta guía completa, te ofreceremos una explicación detallada sobre cómo funciona la recta numérica, cómo se colocan los números y algunos ejemplos prácticos que te ayudarán a dominar este concepto. A lo largo del artículo, también abordaremos distintos tipos de números y su representación en la recta, así como consejos útiles para mejorar tu comprensión.
## ¿Qué es una Recta Numérica?
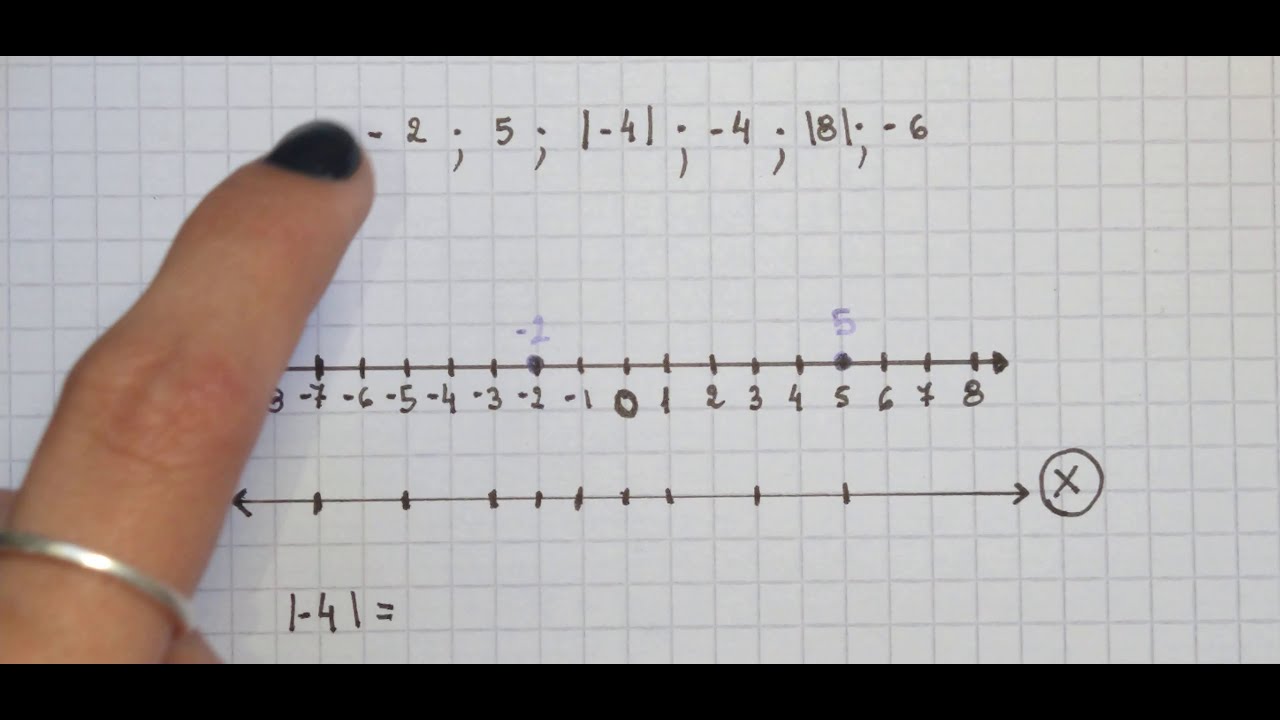
La recta numérica es una línea horizontal en la que se representan números en un orden específico. Esta línea se extiende infinitamente en ambas direcciones, lo que significa que puedes encontrar números negativos a la izquierda del cero y números positivos a la derecha. La recta numérica es fundamental para entender la magnitud y el valor relativo de los números.
### Características de la Recta Numérica
1. Punto de Origen: El cero (0) es el punto de referencia central de la recta numérica. Es el punto donde los números positivos y negativos se encuentran.
2. Dirección: A medida que te mueves hacia la derecha desde el cero, los números aumentan. Por el contrario, al moverte hacia la izquierda, los números disminuyen.
3. Espaciado Uniforme: Los números en la recta numérica están espaciados uniformemente, lo que significa que la distancia entre dos números consecutivos es siempre la misma.
### Ejemplo Práctico
Imagina una recta numérica donde el cero está en el centro. Si colocas el número 1 a la derecha del cero y el número -1 a la izquierda, notarás que ambos están a la misma distancia del cero. Este concepto es crucial para entender los números negativos y positivos en un contexto más amplio.
## Tipos de Números en la Recta Numérica
En la recta numérica, podemos clasificar los números en varias categorías. Cada tipo de número tiene su propia ubicación y características.
### Números Naturales
Los números naturales son aquellos que usamos para contar: 1, 2, 3, 4, etc. En la recta numérica, estos números se encuentran a la derecha del cero.
– Ejemplo: Si queremos ubicar el número 5, simplemente lo colocamos a la derecha del 4, manteniendo la misma distancia entre ellos.
### Números Enteros
Los números enteros incluyen los números naturales, sus opuestos negativos y el cero. Por lo tanto, la recta numérica también incluye -1, -2, -3, etc.
– Ejemplo: Si colocamos -3, estará a la izquierda del -2, y así sucesivamente. La distancia entre -2 y -3 es la misma que entre 2 y 3.
### Números Racionales
Los números racionales son aquellos que se pueden expresar como una fracción de dos enteros. En la recta numérica, estos números pueden ubicarse entre los números enteros.
– Ejemplo: Si consideramos 1/2, lo ubicaremos entre 0 y 1, ya que es un número positivo menor que 1.
### Números Irracionales
Los números irracionales no se pueden expresar como una fracción exacta y tienen decimales que no terminan ni se repiten, como √2 o π. Estos números también se pueden ubicar en la recta numérica, pero su representación es más compleja.
– Ejemplo: √2 es aproximadamente 1.41, por lo que lo ubicaríamos entre 1 y 2, un poco más cerca de 1.
## Cómo Ubicar Números en la Recta Numérica
Ubicar números en la recta numérica puede parecer sencillo, pero hay un proceso que puedes seguir para asegurarte de que lo haces correctamente.
### Paso 1: Identificar el Tipo de Número
Antes de ubicar un número, es importante identificar qué tipo de número es. Esto te ayudará a saber si debes mover hacia la derecha (números positivos) o hacia la izquierda (números negativos).
### Paso 2: Determinar la Posición
Una vez que hayas identificado el tipo de número, determina su posición relativa en relación con otros números conocidos. Si es un número entero, simplemente cuenta desde el cero; si es un número fraccionario o decimal, necesitarás estimar su ubicación.
### Paso 3: Usar Espaciado Uniforme
Recuerda que la distancia entre los números en la recta numérica es siempre la misma. Por ejemplo, si ubicas 1 y 2, asegúrate de que la distancia entre ellos sea igual a la distancia entre 0 y 1.
### Ejemplo de Ubicación
Si deseas ubicar el número 3.5 en la recta numérica, primero ubica 3 y 4. Luego, estima que 3.5 estará a la mitad de la distancia entre esos dos números. Esto te ayudará a visualizar correctamente su posición.
## Práctica con Ejemplos
La práctica es fundamental para dominar la ubicación de números en la recta numérica. Aquí hay algunos ejemplos que puedes seguir.
### Ejemplo 1: Ubicación de Números Enteros
– Ubica -2, 0 y 3 en la recta numérica.
– Comienza con el cero en el centro.
– Coloca -2 a la izquierda del cero.
– Luego, coloca 3 a la derecha del cero.
### Ejemplo 2: Ubicación de Números Racionales
– Ubica 1/4 y 3/4 en la recta numérica.
– Primero, ubica 0 y 1.
– Divide el espacio entre 0 y 1 en cuatro partes iguales.
– Coloca 1/4 en la primera marca y 3/4 en la tercera marca.
### Ejemplo 3: Ubicación de Números Irracionales
– Ubica √3 en la recta numérica.
– Sabemos que √3 es aproximadamente 1.73.
– Ubica 1 y 2 en la recta, y coloca √3 un poco más cerca de 2.
## Consejos para Mejorar la Comprensión
Ubicar números en la recta numérica puede volverse más intuitivo con la práctica. Aquí hay algunos consejos que pueden ayudarte a mejorar tu habilidad.
### Usa Herramientas Visuales
Dibuja tu propia recta numérica en papel o utiliza aplicaciones en línea que te permitan visualizar los números. Esto puede hacer que el proceso sea más interactivo y fácil de entender.
### Practica con Juegos
Hay muchos juegos educativos que pueden ayudarte a practicar la ubicación de números. Busca juegos de matemáticas que se enfoquen en la recta numérica.
### Estudia con Otros
Trabajar en grupo puede ser beneficioso. Explicar cómo ubicas un número a alguien más puede ayudarte a solidificar tu comprensión.
## Preguntas Frecuentes (FAQ)
### ¿Qué es la recta numérica y por qué es importante?
La recta numérica es una línea que representa números en un orden específico, permitiendo visualizar relaciones entre ellos. Es importante porque facilita la comprensión de conceptos matemáticos, como la suma, resta y comparación de números.
### ¿Cómo se representan los números negativos en la recta numérica?
Los números negativos se representan a la izquierda del cero en la recta numérica. Cuanto más lejos te alejas del cero hacia la izquierda, menor es el valor del número.
### ¿Puedo ubicar fracciones en la recta numérica?
Sí, las fracciones se pueden ubicar en la recta numérica. Debes determinar su valor decimal y luego ubicarla entre los números enteros correspondientes.
### ¿Cuál es la diferencia entre números racionales e irracionales?
Los números racionales son aquellos que se pueden expresar como una fracción de dos enteros, mientras que los números irracionales no pueden representarse como fracciones exactas y tienen decimales que no terminan ni se repiten.
### ¿Cómo puedo mejorar mi habilidad para ubicar números?
Practicar con herramientas visuales, juegos educativos y trabajar en grupo puede ayudarte a mejorar tu habilidad para ubicar números en la recta numérica.
### ¿Es útil la recta numérica en niveles avanzados de matemáticas?
Sí, la recta numérica es fundamental en niveles avanzados de matemáticas, ya que ayuda a comprender conceptos más complejos como funciones, ecuaciones y análisis gráfico.
### ¿Cómo se ubican los números decimales en la recta numérica?
Los números decimales se ubican entre los números enteros en la recta numérica. Por ejemplo, 0.5 se colocaría entre 0 y 1, a la mitad de la distancia entre esos dos números.
La recta numérica no solo es una herramienta para visualizar números, sino también un puente para entender conceptos más complejos en matemáticas. Al practicar su uso, te volverás más hábil en la resolución de problemas y en la comprensión de las relaciones numéricas.